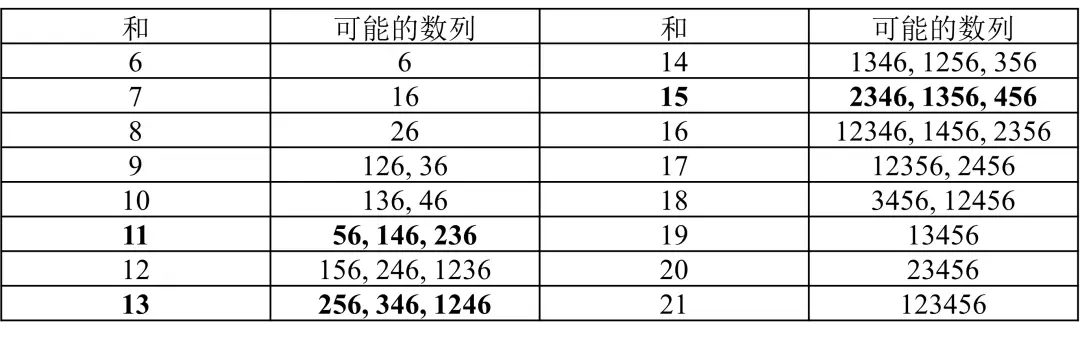
何夕老师为大家带来了一套由其编写的纸笔谜题,主题为 Blurred Vision。
在这一套谜�题中,每道题目都有若干线索不可见,你需要在解题的同时,确定这些线索。
今天是该系列的第四题,纸笔类型为 Skyscraper (Diagonal, Sum)。
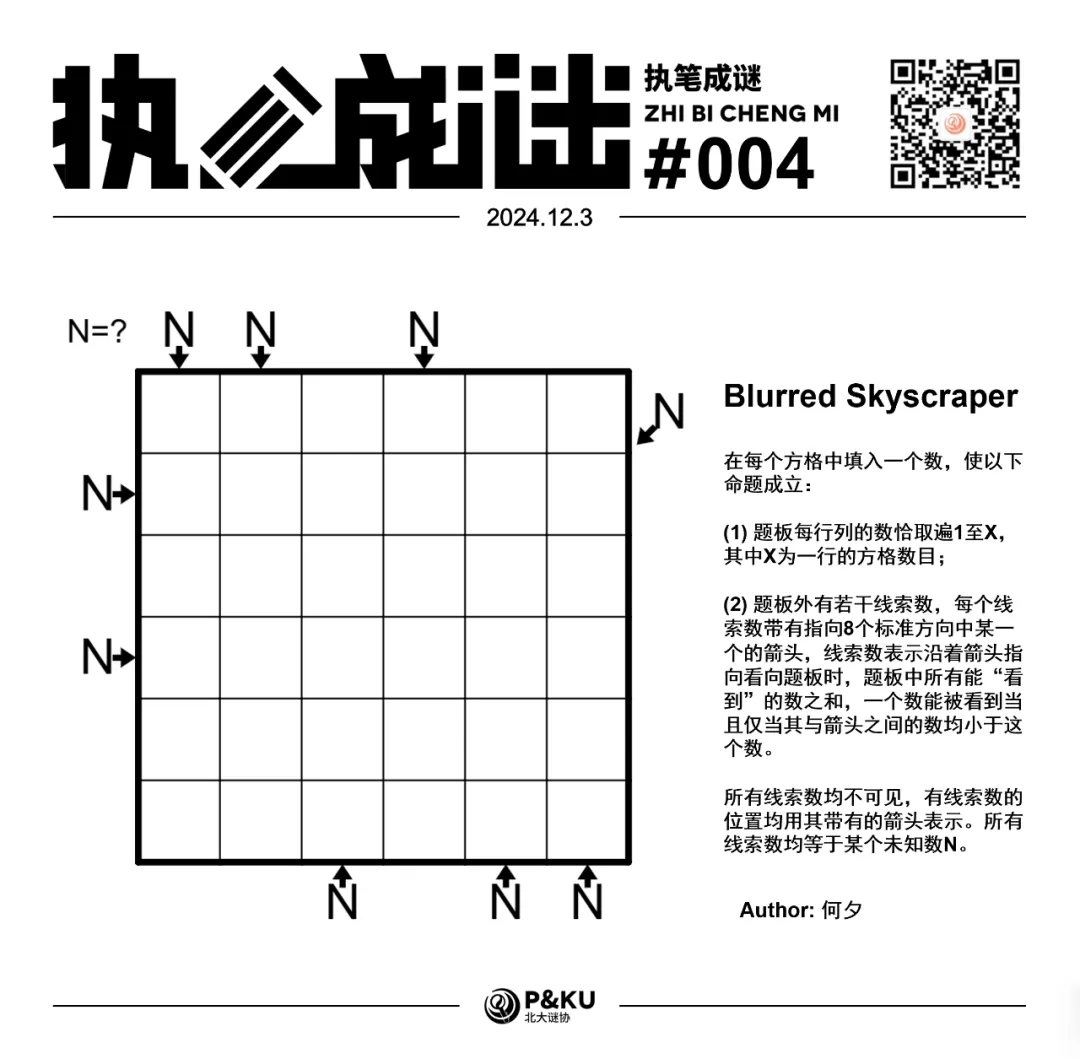
Skyscraper 规则
在每个方格中填入一个数,使以下命题成立:
- 题板每行列的数恰取遍 1 至 X,其中 X 为一行的方格数目;
- 题板外有若干线索数,每个线索数带有指向 8 个标准方向中某一个的箭头,线索数表示沿着箭头指向看向题板时,题板中所有能“看到”的数之和,一个数能被看到当且仅当其与箭头之间的数均小于这个数。
所有线索数均不可见,有线索数的位置均用其带有的箭头表示。所有线索数均等于某个未知数 N。
做题链接
你可以在 penpa 网站上进行尝试
答案验证
(作者:何夕)
步骤解析
查看步骤解析
首先想必各位都能意识到我们需要决定 N 的取值。
观察最上方的 3 个箭头,意味着我们需要考虑至少存在 3 个首个数字不同的,同时和相同的递增数列。
同时注意�最后一位必须是 6。此处我们大概列举一下:
因此 N 的取值只能是 11,13 或者 15。
首先看 N=11 的情形,我们先通过交换部分列的顺序,让 6 按下图的方式排布以便分析。
显然第一及第六列的箭头如图所示,且必然会看到 5,因此这两列的分解方式必然是 56。
但此时第二列无论哪个方向都无法恰看到和为 11 的数。故这种情形不成立。
接下来看 N=13 的情形。我们同样先通过交换部分列的顺序,让 6 按下图的方式排布。
第一、二、五、六列只能从图示的方向看到和为 13 的数,且由于第一及第六列能看到 5,故必然以 2 开始。
由于只有一种包含 5 的分解方式,故第二及第五列不能看到 5。此时第一及第六行的 4 只能放在灰色格子中。
但剩余的分解方式均包含 4,且均不以 4 开始,故这两列无法看到和为 13 的数,这种情形也不成立。
因此 N 只能为 15。我们同样先通过交换部分列的顺序,让 6 按下图的方式排布。
对于从上方看到 1356 的那一列,3 必然出现在第二行,故看到 2346 那一列的 3 只能出现在第三行,那一列的数字排布只能是 213465。
由此得到下图。
假设从上放看去 1356 位于第三列,则得到下图,此时最后一列的三个箭头中一个会首先看到 3,无法成立。
由此得到 1356 位于第一及第六列,456 位于第三及第四列。通过简单分析并可能地再次交换第三及第四列得到下图。
对于圆中的数字,只能是 135 中的某一个。
由于它需要是某种分解方式中的首位,故其只能为 1,分解方式为 1356,由此得到第一、二、六列的顺序。
对于正方形中的数字,其只能是 246 中的某一个。由于其不能被看见,故其为 2。
由此得到前四列的顺序。最后通过剩余的两个箭头即可填完盘面。