【执笔成谜】彼岸双生——Kurotto篇

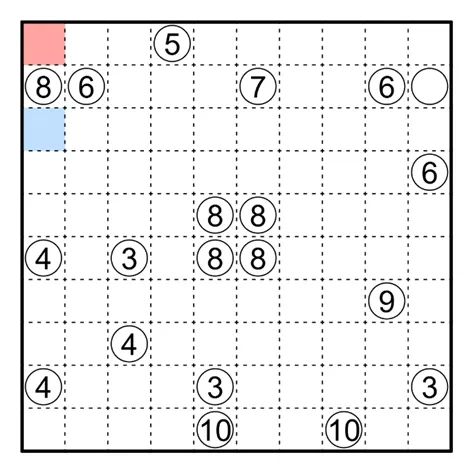
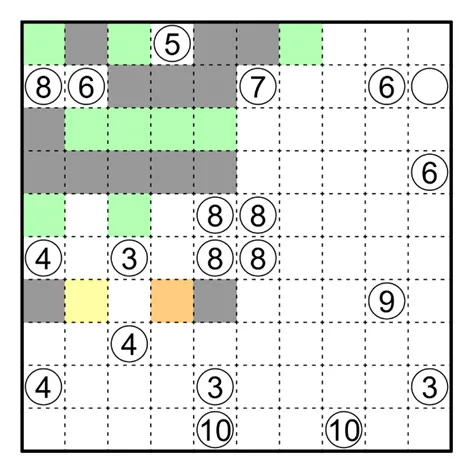
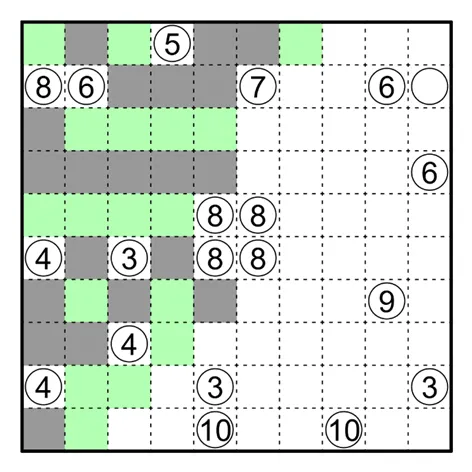
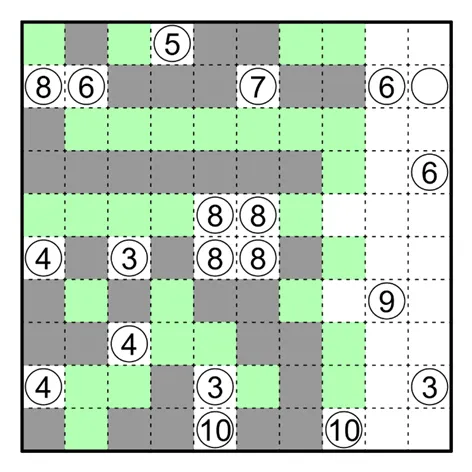
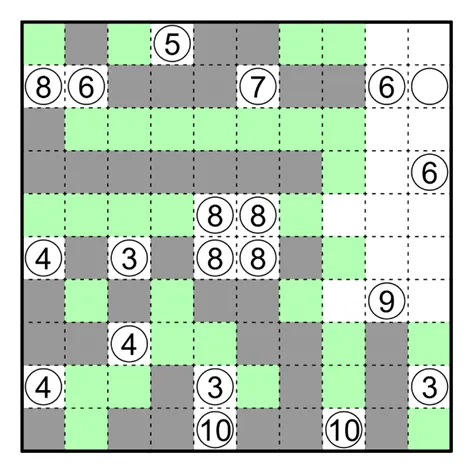
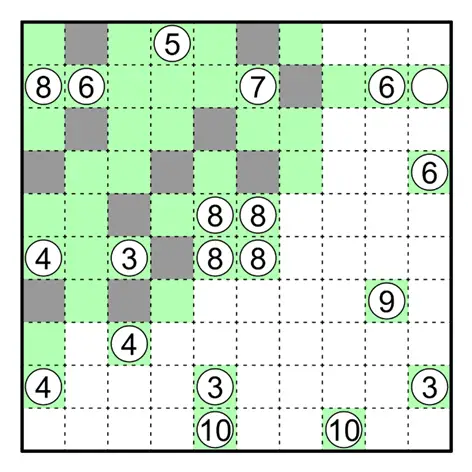
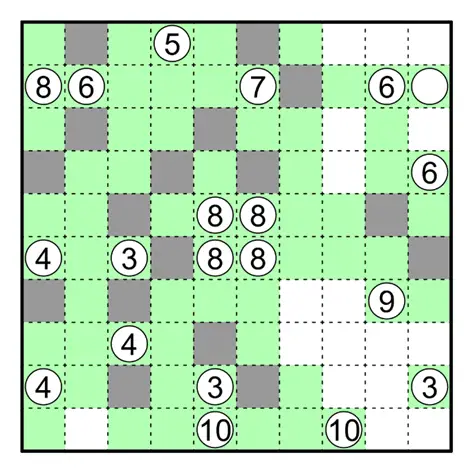
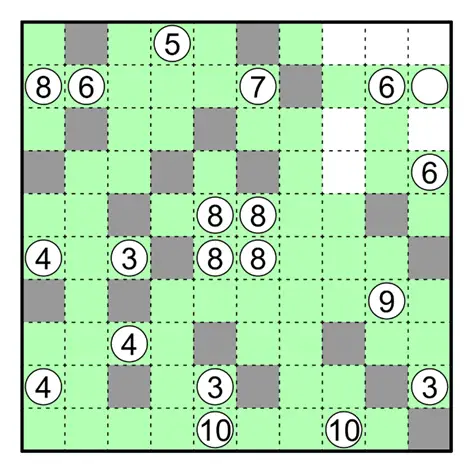
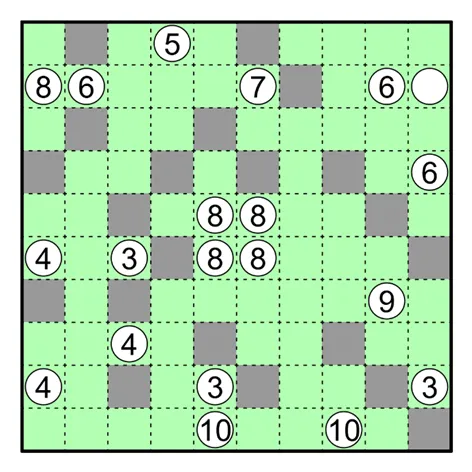
何夕老师为大家带来了一套由其编写的纸笔谜题，主题为 Hidden Twins（彼岸双生）。 在这一套谜题中，每道题目在原规则盘面能得到一个解的同时，在另一个规则下能得到另一个解， 你需要在解出原题之后，确定被隐藏的规则，并且以隐藏的规则再解一遍。

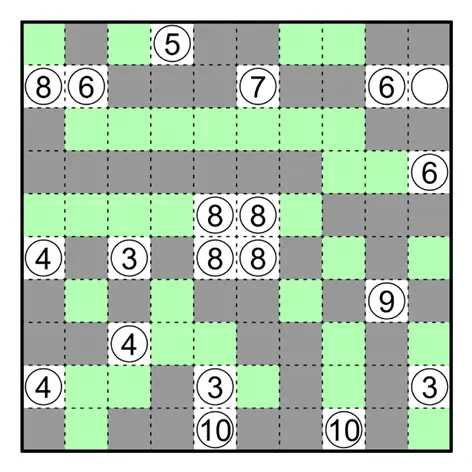
今天是该系列的第八题（也是最后一题），至此彼岸双生系列的题目已全部放出。本题原规则盘面的纸笔类型为凝块。

Kurotto 凝块规则

涂黑一些空格。数字表示与此格相邻的所有涂黑的连通组的总面积。

另一个规则能保证在 2024 年世界谜题锦标赛中出现过。 你可以查看 2024 年世界谜题锦标赛题型的英文版说明链接。

做题链接

你可以在 penpa 网站上进行尝试

答案验证

输入答案以验证

依次输入每一行的黑格数，多位数只填写个位。

隐藏规则

隐藏规则

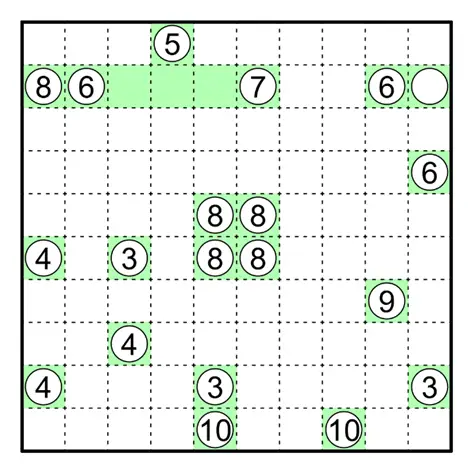
田鼠挖洞（Kurodoko）

涂黑一些格子，使得涂黑的格子之间不相邻，且留白的格子连通成一个整体。 白圈里的数字必须在留白格里，并表示此格横竖能够直接连接到且不被涂黑格阻挡的留白格个数，包括此格本身。

解答

（作者：何夕）

步骤解析

查看步骤解析

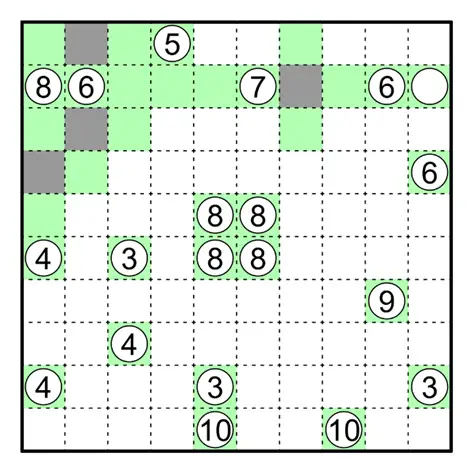
极值逻辑与面积大小加减在凝块中十分常见。通过已知面积之和的两块区域中一块的最大值，可以得到另一块的最小值。 因此距离较近而差距较大的提示数在凝块中十分重要。

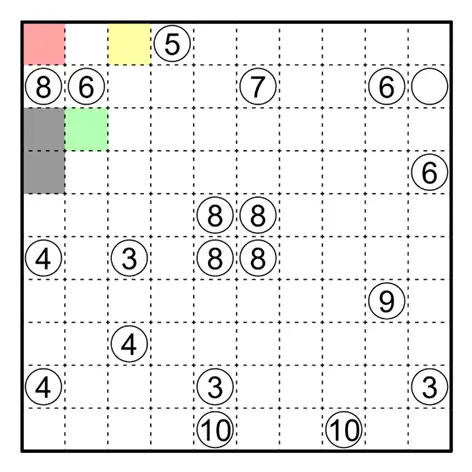
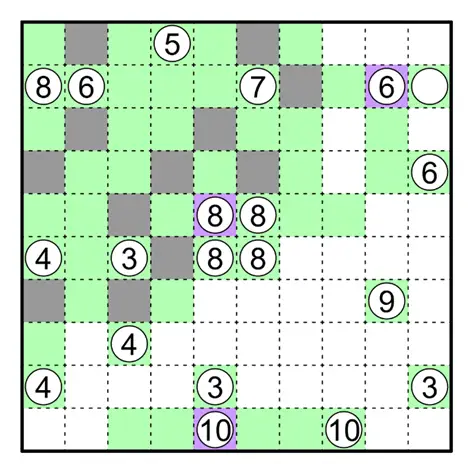
在下图中，红色方格延伸出的区域面积至多为 5，因此蓝色区域面积至少为 3，且不能直接相右延伸。 因为否则红色区域也需要延伸（其面积至少为 2），此时 ⑧ 相邻的区域均与 ⑥ 相邻，矛盾。

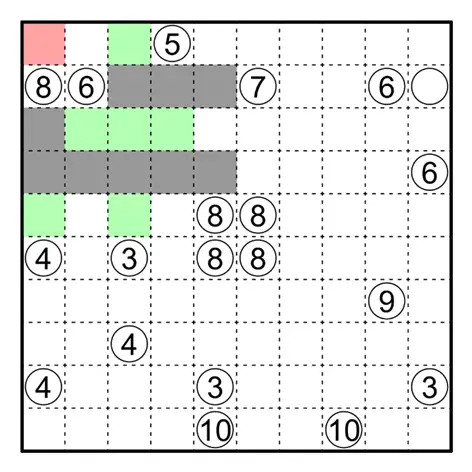
下图黄色方格不能涂黑，否则 ⑥ 相邻的区域均与 ⑤ 相邻，矛盾。因此红色方格所在区域面积至多为 2,⑧ 下方的区域面积至少为 6。

注意到 ⑥ 右侧区域面积为 5，因此其上方方格需要涂黑，且其面积为 1。

对于下图中的红色与蓝色方格，通过与第一步中类似的逻辑得到蓝色方格均需要涂黑。

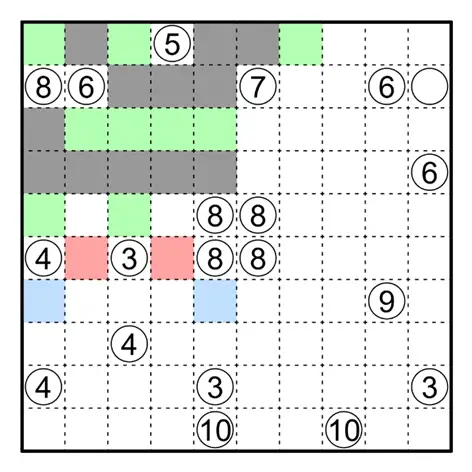
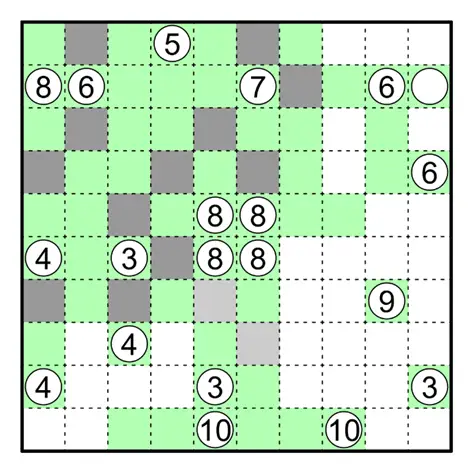
下图中的黄色方格不能涂黑。否则 ③ 无法向左或右延伸，因为这会导致 ④ 周围的区域均与 ③ 相邻， 同时 ③ 也无法向右延伸面积为 3 的区域，因为这会导致 ⑧ 周围的区域均与 ③ 相邻。同样的逻辑可以得到橙色方格不能涂黑。

由此可以确定 ③ 周围黑格的情况，并得到一些简单的推论。

容易发现如果 ⑩ 右侧的面积为 3 的区域不与 ⑨ 相邻的话，⑨ 无法向上延伸出 9 格区域而使右侧的 ⑥ 成立。得到下图。

由于右侧的 ⑥ 至少与上方的 ⑥ 共用面积为 2 的区域，且这部分面积无法与 ⑨ 共用， 因此前者至多与 ⑨ 共用面积为 4 的区域，⑨ 还需要的两个区域只能通过下图中的方式得到。

步骤解析 隐藏规则

查看步骤解析

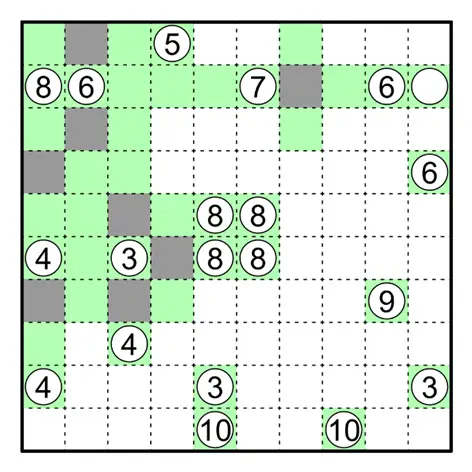
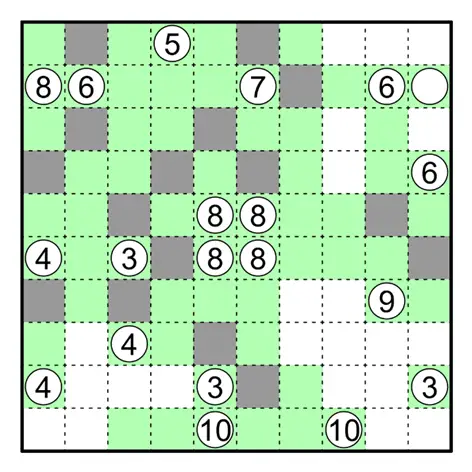
极值逻辑与大小加减在田鼠挖洞中同样常见。对于左上角的 ⑧，其纵向至多看到 4 格，否则就会与下方的 ④ 相连导致其看到 5 格。 由此得到其向右至少看到 5 格，得到下图。

通过一些简单的逻辑得到下图。

用与第一步中一样的方格对左侧中间的 ④ 进行分析，得到下图。

分析上方 ⑤ 所看到的方格，发现情形唯一，得到下图。（同时可以得到 ⑦ 的情形）

对下图中紫色标记出的线索数进行分析，得到下图。

如果中央左上方的 ⑧ 纵向上看到 3 格，那么右上方的 ⑧ 同样在纵向上看到 3 格（它们在横向上看到同样多的方格，这种分析方法在田鼠挖洞中十分常见）由此得到下图。 注意到 ③ 此时看到 4 格，矛盾。

由此得到下图。中央的 ⑧ 均在水平方向上看到 5 格，竖直方向上看到 4 格。

之后通过一些简单的逻辑得到最终答案。